Surface Force: Air Drag
1. Overview
1. Functions
AirDragclass inheritsSurfaceForcebase class and calculates air drag disturbance force and torque.
2. Related files
air_drag.cpp,air_drag.hpp: TheAirDragclass is defined.surface_force.cpp,surface_force.hpp: The base classSurfaceForceis defined.- Note:
SurfaceForceclass inheritsSimpleDisturbanceclass, andSimpleDisturbanceclass inheritsDisturbanceclass. So, please refer them if users want to understand the structure deeply.
- Note:
disturbance.ini: Initialization file
3. How to use
- Make an instance of the
AirDragclass inInitializeInstancesfunction indisturbances.cpp- Create an instance by using the initialization function
InitAirDrag
- Create an instance by using the initialization function
- Set the parameters in the
disturbance.ini- Select
ENABLEforcalculationandlogging - Select the following conditions of air drag calculation
- Surface Temperature degC
- Atmosphere Temperature degC
- Molecular weight of the thermosphere g/mol
- Select
2. Explanation of Algorithm
1. CalcCoefficients
1. overview
CalcCoefficientscalculates the normal and in-plane coefficients forSurfaceForcecalculation. The air drag force acting on a surface is expressed as the following equation
\[ \begin{align} \boldsymbol{F}=-C_{n}\boldsymbol{n}+C_{t}\boldsymbol{t}\\ C_{n}=\frac{1}{2}\rho A v^2 C_{n}^{\prime}\\ C_{t}=\frac{1}{2}\rho A v^2 C_{t}^{\prime} \end{align} \]
- This function mainly calculates the common part of the coefficient calculation. $C_{n}^{\prime}$ and $C_{t}^{\prime}$ are calculated in
CalCnCtfunction, and they will be used in this function.
2. inputs and outputs
- input
- $\boldsymbol{v}$: Relative velocity vector between the spacecraft and the atmosphere [m/s]
- $\rho$: air density [kg/m3]
- output
- coefficients $C_{n}$ and $C_{t}$
3. algorithm
- See above equations.
4. note: NA
2. CalCnCt
1. overview
CalCnCtcalculates $C_{n}^{\prime}$ and $C_{t}^{\prime}$.
2. inputs and outputs
- input variables
- $\boldsymbol{v}$: Relative velocity vector between the spacecraft and the atmosphere [m/s]
- Currently, we assume that this value equals spacecraft velocity in the body-fixed frame.
- $\boldsymbol{v}$: Relative velocity vector between the spacecraft and the atmosphere [m/s]
- input parameters
- $\sigma_{d}$: Diffuse coefficients for air drag
- Ini file provide specularity for air drag $\sigma_{s}$, and the diffuse coefficient is derived as $\sigma_{d}=1-\sigma_{s}$.
- Note: There is no absorption term for air drag. Thus total reflectivity is set as 1.
- $T_{w}$: Temperature of the surface [K]
- $T_{m}$: Temperature of the atmosphere [K]
- $M$: Molecular weight of the thermosphere [g/mol]
- In the default ini file, we use $M=18$, and it is a little bit smaller than the molecular weight of atmosphere $M=29$. Structure of the Thermosphere provides information on the molecular weight of the thermosphere.
- $\sigma_{d}$: Diffuse coefficients for air drag
- outputs
- $C_{n}^{\prime}$ and $C_{t}^{\prime}$
3. algorithm
- $C_{n}^{\prime}$ and $C_{t}^{\prime}$ are calculated as following equations
\[ \begin{align} C_{n}^{\prime} &= \frac{2-\sigma_{d}}{\sqrt{\pi}}\frac{\Pi(S_{n})}{S^{2}}+\frac{\sigma_{d}}{2}\frac{\chi(S_{n})}{S^{2}}\sqrt{\frac{T_{w}}{T_{m}}}\\ C_{t}^{\prime} &=\frac{\sigma_{d}}{\sqrt{\pi}}\frac{\chi(S_{n})}{S^{2}}S_{t} \end{align} \]
- $S, S_{n}, S_{t}$ are defined as follows
- $k=1.38064852E-23$ is the Boltzmann constant
- $\theta$ is the angle between the normal vector and the velocity vector
- $\cos{\theta}$ and $\sin{\theta}$ are calculated in
SurfaceForcebase class.
\[ \begin{align} S &= \sqrt{\frac{Mv^{2}}{2kT_{w}}}\\ S_{n} &= S\cos{\theta}\\ S_{t} &= S\sin{\theta}\\ \end{align} \]
- $\Pi(x)$ and $\chi(x)$ are defined as follows
- where
erfis the Gauss error function. - These functions are defined as
CalcFunctionPiandCalcFunctionChi.
- where
\[ \begin{align} \Pi(x) &= x e^{-x^{2}}+\sqrt{\pi}(x^2+0.5)(1+erf(x))\\ \chi(x) &= e^{-x^{2}}+\sqrt{\pi}x(1+erf(x)) \end{align} \]
4. note
- Please see the reference document for more information on detailed calculations.
3. Results of verifications
1. Verification of magnitude of the force
1. overview
- The calculated magnitude of the air drag force is compared with other calculation results in three cases.
2. conditions for the verification
- See the bottom table.
3. results
-
The calculation result is completely the same as the other calculation.
parameters/results Case 1 Case 2 Case 3 $\sigma_{d}$ 0.8 0.6 0.4 $\theta$ rad 0.202 0.202 0.202 $v$ m/s 7420 7420 7420 Out-plane force (S2E) 2.30297 2.68680 3.07062 Out-plane force (reference) 2.30297 2.68680 3.07062 Out-plane force (S2E) 0.31514 0.23636 0.15757 Out-plane force (reference) 0.31514 0.23636 0.15757
1. Verification of direction of the force
1. overview
- Next, we confirmed that the direction of the calculated force is correct.
2. conditions for the verification
- S2E is executed using the default setting.
3. results
- We confirmed that the direction of the force is opposite the direction of the velocity of the spacecraft.
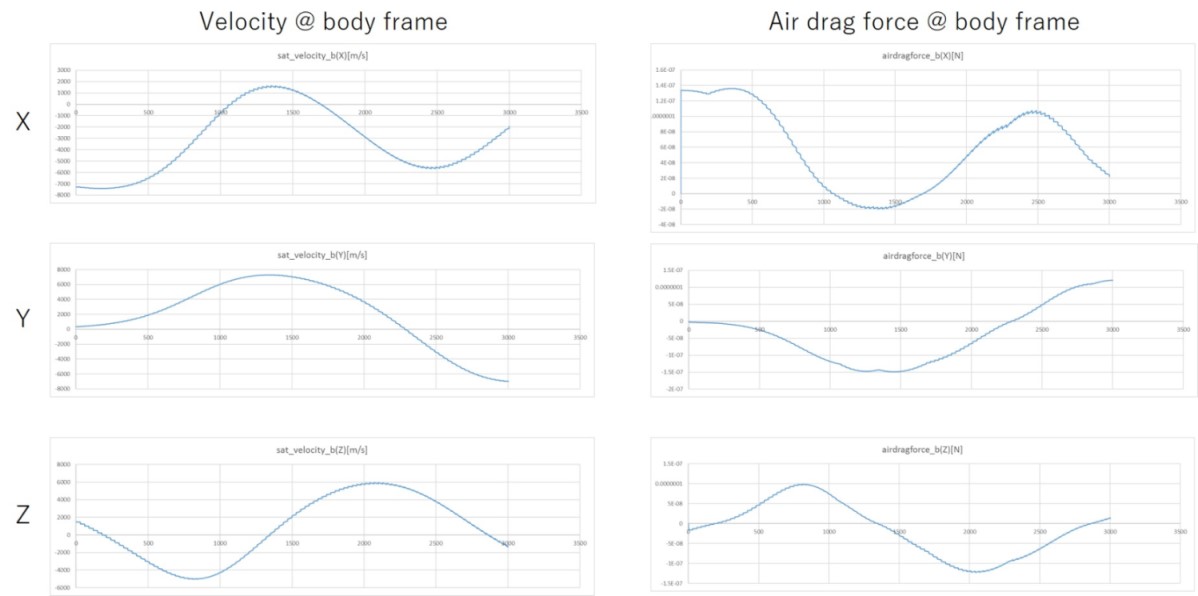
4. References
- H. Klinkrad and B. Fritsche, "ORBIT AND ATTITUDE PERTURBATIONS DUE TO AERODYNAMICS AND RADIATION PRESSURE", in ESA Workshop on Space Weather, 1998.
- Marcel Nicolet, Structure of the Thermosphere, Planetary and Space Science, 1961
- Gauss error function