Specification for Orbit dynamics with RK4 propagation

1. Overview

1. functions

  • The Rk4OrbitPropagation class calculates the position and velocity of satellites with 4th Order Runge-Kutta method(RK4).

2. files

  • src/dynamics/orbit/orbit.hpp, cpp
    • Definition of Orbit base class
  • src/dynamics/orbit/initialize_orbit.hpp, .cpp
    • Make an instance of orbit class.
  • src/dynamics/orbit/rk4_orbit_propagation.hpp, .cpp

3. How to use

  • Select propagate_mode = RK4 in the spacecraft's ini file.
  • Select initialize_mode as you want.
    • DEFAULT : Use default initialize method (RK4 and ENCKE use position and velocity, KEPLER uses init_mode_kepler)
    • POSITION_VELOCITY_I : Initialize with position and velocity in the inertial frame
    • ORBITAL_ELEMENTS : Initialize with orbital elements

2. Explanation of Algorithm

1. Propagate function

  • The position and velocity of the satellite are updated by using RK4. As the input of RK4, the six-state variables are set. These state variables are the three-dimensional position [$x$, $y$ ,$z$] and three-dimensional velocity [$v_x$, $v_y$, $v_z$] at the inertial coordinate. Here, the inertial coordinate is decided by the PlanetSelect.ini
  • As the force which works to the satellite motion is the external acceleration [$a_x$,$a_y$,$a_z$] calculated from the disturbance class or thruster class and the gravity force from the center planet, which is defined in PlanetSelect.ini. As a summary, the orbit is calculated as the following equation. \[ \begin{align} \dot{x} &= v_x\\ \dot{y} &= v_y\\ \dot{z} &= v_z\\ \dot{v}_x &= a_x-\mu\frac{x}{r^3}\\ \dot{v}_y &= a_y-\mu\frac{y}{r^3}\\ \dot{v}_z &= a_z-\mu\frac{z}{r^3}\\ r &= \sqrt{x^2+y^2+z^2} \end{align} \]

3. Results of verifications

1. Verification of the error of Fourth Order Runge-Kutta method (RK4)

1. Overview

  • Verify the numerical integration error of the RK4 method.
  • The output of the simulation was compared with the analytical solution.

2. conditions for the verification

  • The Verifications were conducted in the case of simulation_step_s and orbit_update_period_s were 0.1(sec), 1(sec), and 10(sec).
  • The initial values of the propagation are as follows: 
    initial_position_i_m(0) = 1.5944017672e7
initial_position_i_m(1) = 0.0
initial_position_i_m(2) = 0.0

initial_velocity_i_m_s(0) = 0.0
initial_velocity_i_m_s(1) = 5000.0
initial_velocity_i_m_s(2) = 0.0
  • This is a circular orbit, which period is about 20040(sec). The center of the orbit is Earth.
  • As a reference, the analytical solution was used. The solution is as follows: \[ x=R\cos(\omega t),y=R\sin(\omega t)\quad when~R=1.5944017672\times10^7, \omega=0.000313597243985794 \]
  • All of the effects of disturbance and environment were disabled.
  • The simulation time is 60120(sec), which is approximately three-period. In addition, for a long-term test, the case in which simulation time is 200400(about 10 periods) was tested. The orbit_update_period_s of this case is 1(sec).

3. results

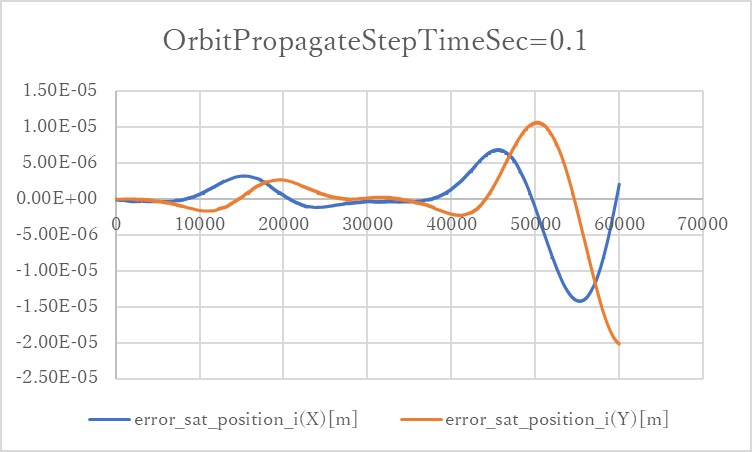
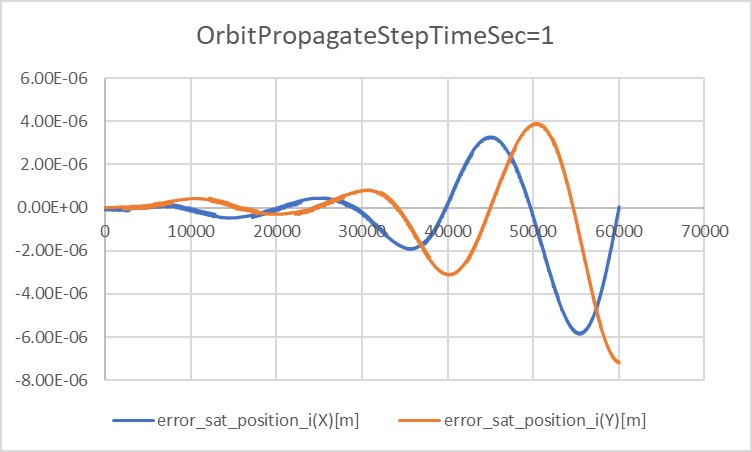
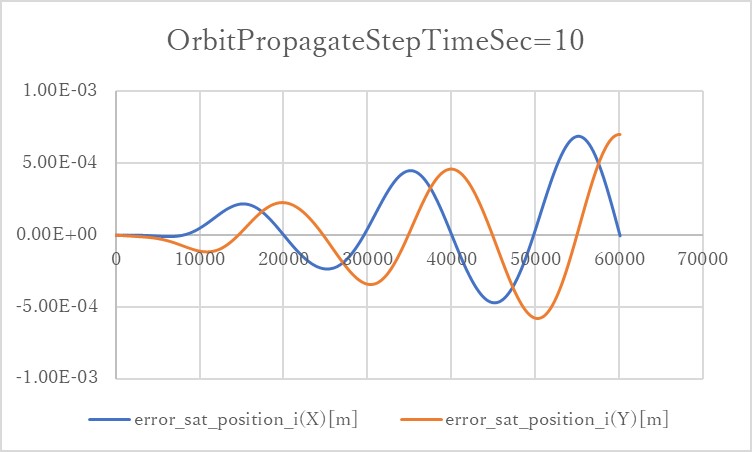
orbit_steptimesec_01 orbit_steptimesec_1 orbit_steptimesec_10
  • In the cases of orbit_update_period_s=0.1 and orbit_update_period_s=1, the error is kept within $10^{-6}$ order. However, once the error grows, it will get bigger and bigger.
  • In the case of orbit_update_period_s=10, the error quickly grows up to $10^{-4}$ order.
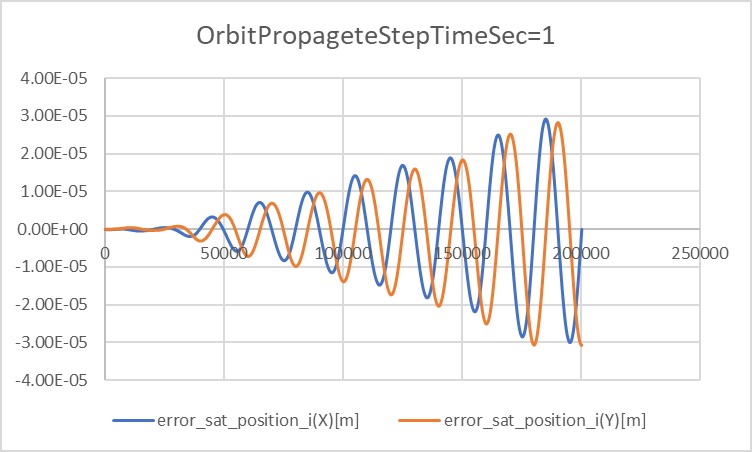
orbit_steptimesec_1_longterm
  • In the long-term test result, it is clear that the error magnitude grows proportionally to the time.

4. Others

  • At first, the output of STK would be used for reference. However, it did not work well. Data were input as follows:
orbit_STKsettings
  • However, the result is as follows:
orbit_STKresult
  • As this figure shows, the initial values in the result are slightly different from the input.
    • In the .sa files, the initial values of $x, y, z, v_x, v_y, v_z$ are converted into elements of orbit and stored. The error might occur in the process of this conversion.

4. References

NA