Specification of Third Body Gravity Disturbance Calculation
1. Overview
1. Functions
- The
ThirdBodyGravityclass calculates the gravity acceleration generated by the third body, such as Sun, Moon, or planets.
2. Related files
src/disturbance/third_body_gravity.cppsrc/disturbance/third_body_gravity.hpp
3. How to use
- Make an instance of the
ThirdBodyGravityclass inInitializeInstancesfunction indisturbances.cpp- Create an instance by using the initialization function
InitThirdBodyGravity
- Create an instance by using the initialization function
- Chose a orbit propagator mode that considers disturbances.
- Edit the
disturbance.inifile- Select
ENABLEforcalculationandlogging - Select
number_of_third_bodyandthird_body_nameyou need. - NOTE: All of the
third_body_nameobjects must be included in theselected_body_nameof the[CELESTIAL_INFORMATION]section in thesimulation_base.ini.
- Select
- NOTE: When the class
ThirdBodyGravityis instantiated, the class reports an error in the following cases.- The target specified by
center_objectof the[CELESTIAL_INFORMATION]section in thesimulation_base.ini. is included in the list ofthird_body. - The list of
third_body_nameincludes objects which are not in the list ofselected_body_namein the[CELESTIAL_INFORMATION]section in thesimulation_base.ini.
- The target specified by
- NOTE: If the same body is specified more than once in the list of
third_body_nameindisturbance.ini, the second and subsequent entries of the body are ignored.
2.Explanation of Algorithm
- The base algorithm is referred to Satellite Orbits chapter 3.3.
1. CalcAcceleration_i_m_s2 function
1. overview
- This function calculates the acceleration in the inertial frame generated by the third body.
2. inputs and outputs
-
Input
- position of the third body seen from the center object in the inertial coordinate system
- position of the third body seen from the spacecraft in the inertial coordinate system
- gravity constant (GM) of the third body
- NOTE: These inputs are derived from
CelestialInformation.
-
Output
- acceleration generated by the third body in the inertial coordinate system
3. algorithm
- Definition of the variables
- $\boldsymbol{r}$: the position of the spacecraft (written as
sc_position_i_min the code) - $\boldsymbol{s}$: the position of the third body (written as
third_body_pos_i_min the code) - $\boldsymbol{s}-\boldsymbol{r}$: the position of the third body seen from the spacecraft (written as
third_body_position_from_sc_i_min the code)
- $\boldsymbol{r}$: the position of the spacecraft (written as
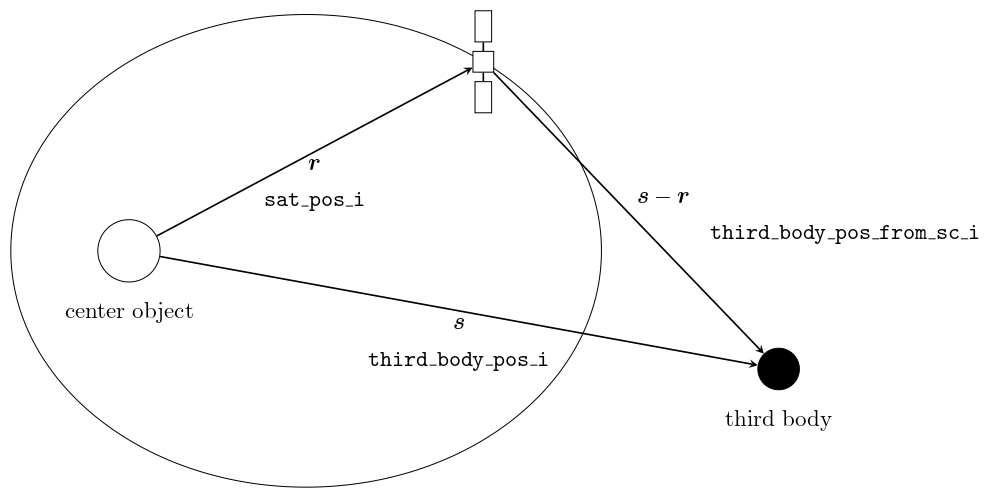
- The acceleration disturbance effect by the third body is written as follows:
\[ \ddot{\boldsymbol{r}}=GM\left(\frac{\boldsymbol{s}-\boldsymbol{r}}{|\boldsymbol{s}-\boldsymbol{r}|^3}-\frac{\boldsymbol{s}}{|\boldsymbol{s}|^3}\right) \]
- See section 3.3.1 of Satellite Orbits for a detailed explanation.
3. Results of verifications
1. overview
- The deformation of the orbit caused by the acceleration of the third body gravity is compared between S2E and STK.
2. conditions for the verification
-
input files
- Default initialize files
-
initial values
simulation_start_time_utc = 2020/01/01 11:00:00.0 simulation_duration_s = 86400 simulation_step_s = 10 orbit_update_period_s = 10 log_output_period_s = 5 simulation_speed_setting = 0-
Since the effect of third body gravity increases as one moves away from the central object, it is verified for GEO.
initial_position_i_m(0) = 42241095.67425744 initial_position_i_m(1) = 0 initial_position_i_m(2) = 0 initial_velocity_i_m_s(0) = 0 initial_velocity_i_m_s(1) = 2.978E+4 initial_velocity_i_m_s(1) = 3071.859163190527-
All the disturbance calculations, except for the third-object gravity, are set to DISABLE.
-
The following cases are tested.
- Only the gravity of the Sun is taken into account
- Only the gravity of the Moon is taken into account
- Both the gravity of the Sun and the Moon are taken into account
- Only the gravity of Mars is taken into account (TBW)
-
-
- results
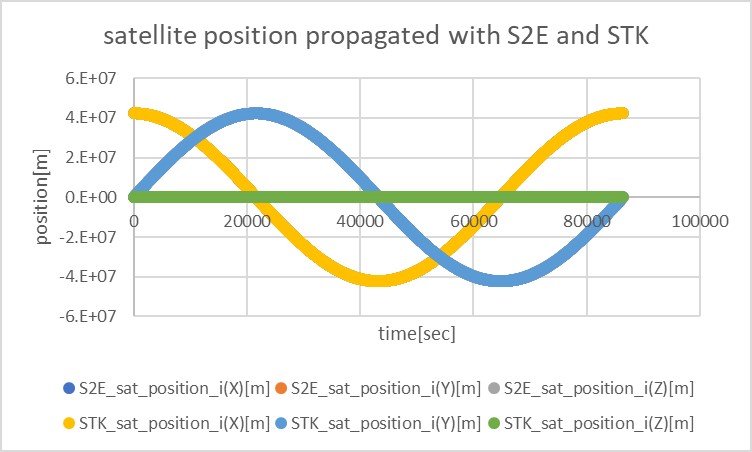
- Without the third body, S2E and STK show the same result.
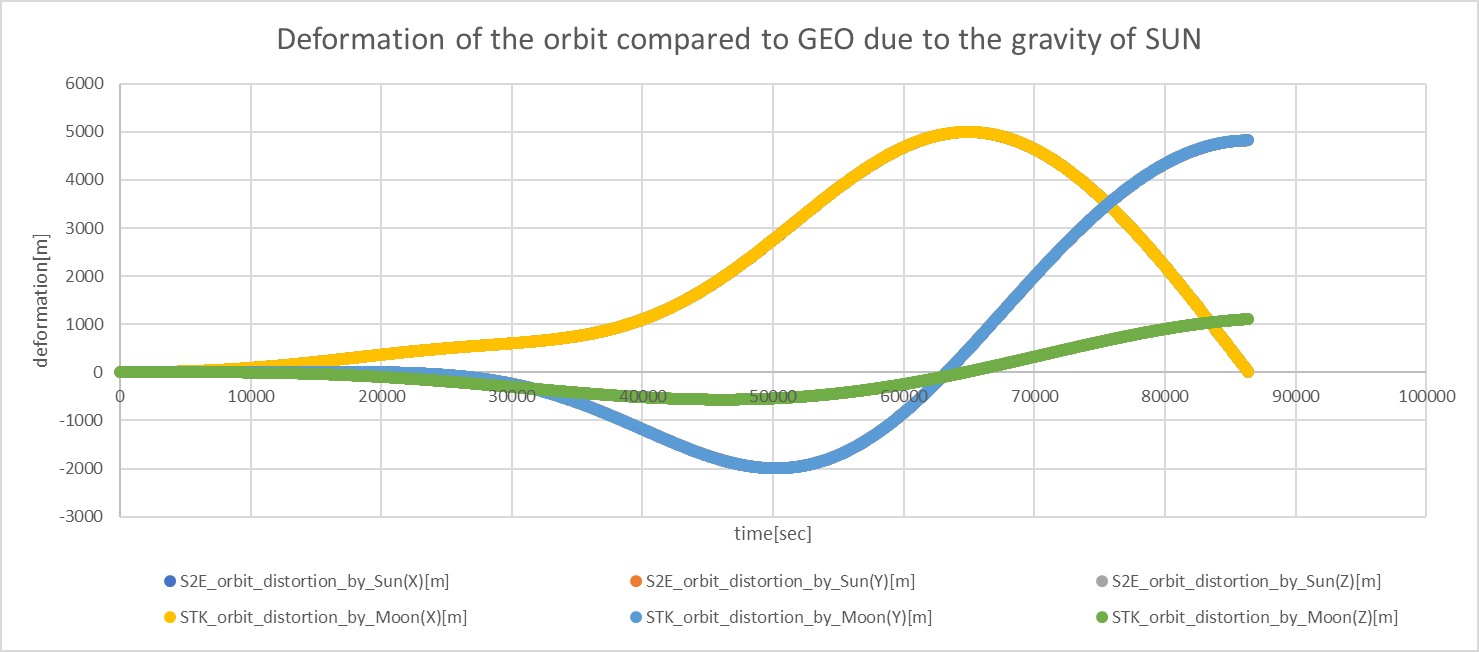
- Only the gravity of the Sun is taken into account
- The deformation of the orbit compared to GEO is shown in the following figure.
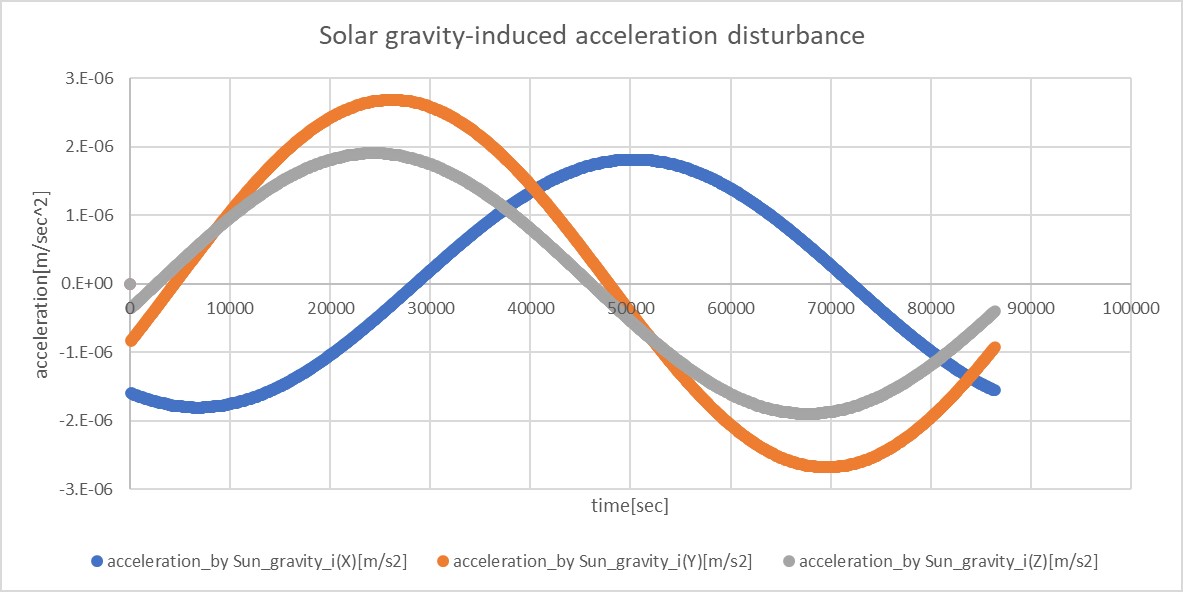
- The acceleration disturbance caused by the Sun's gravity is shown in the following figure.
- Only the gravity of the Moon is taken into account
- The deformation of the orbit compared to GEO is shown in the following figure.
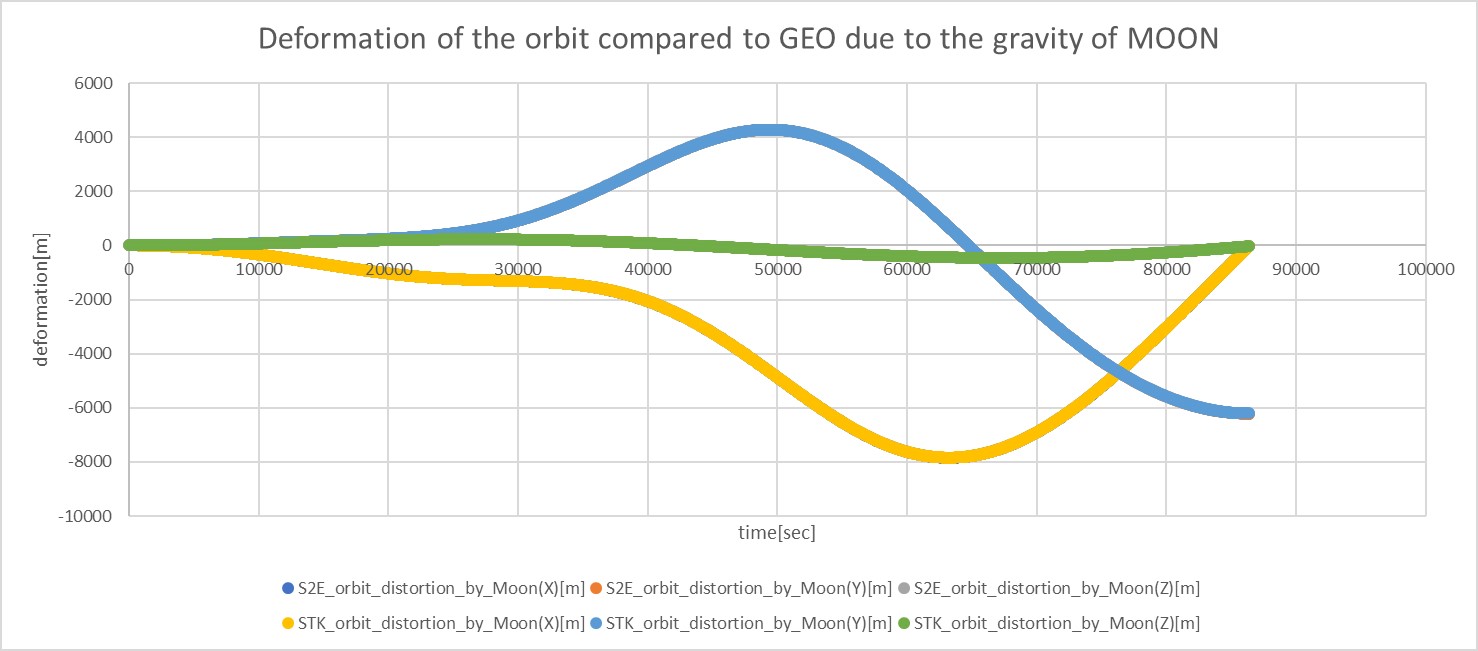
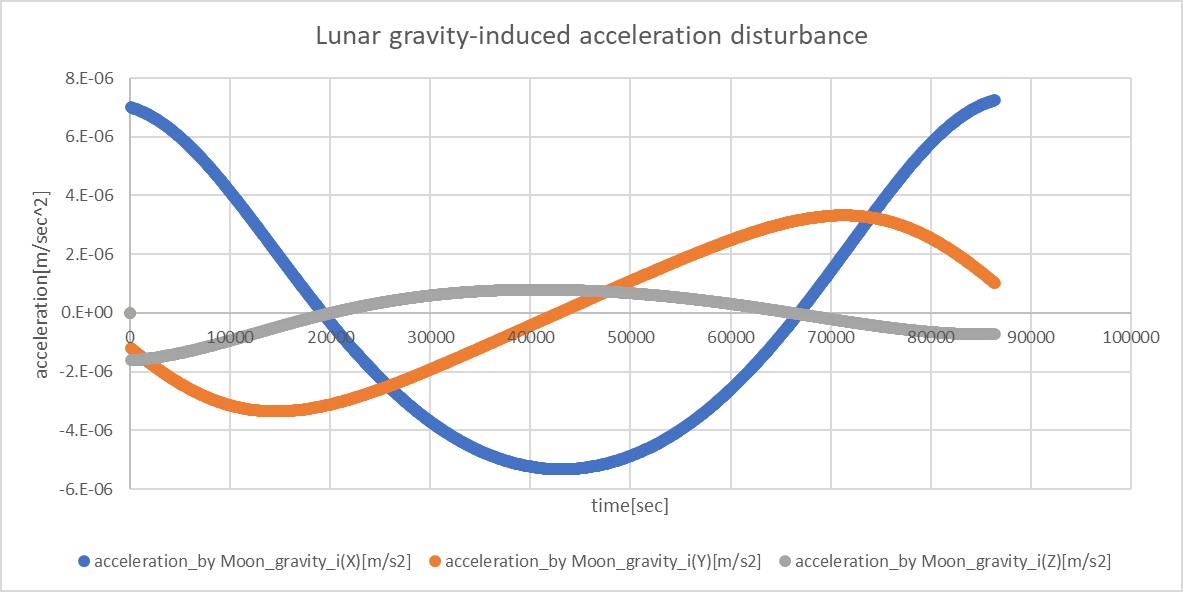
- The acceleration disturbance caused by the Moon's gravity is shown in the following figure.
- Both the gravity of the Sun and the Moon are taken into account
- The deformation of the orbit compared to GEO is shown in the following figure.
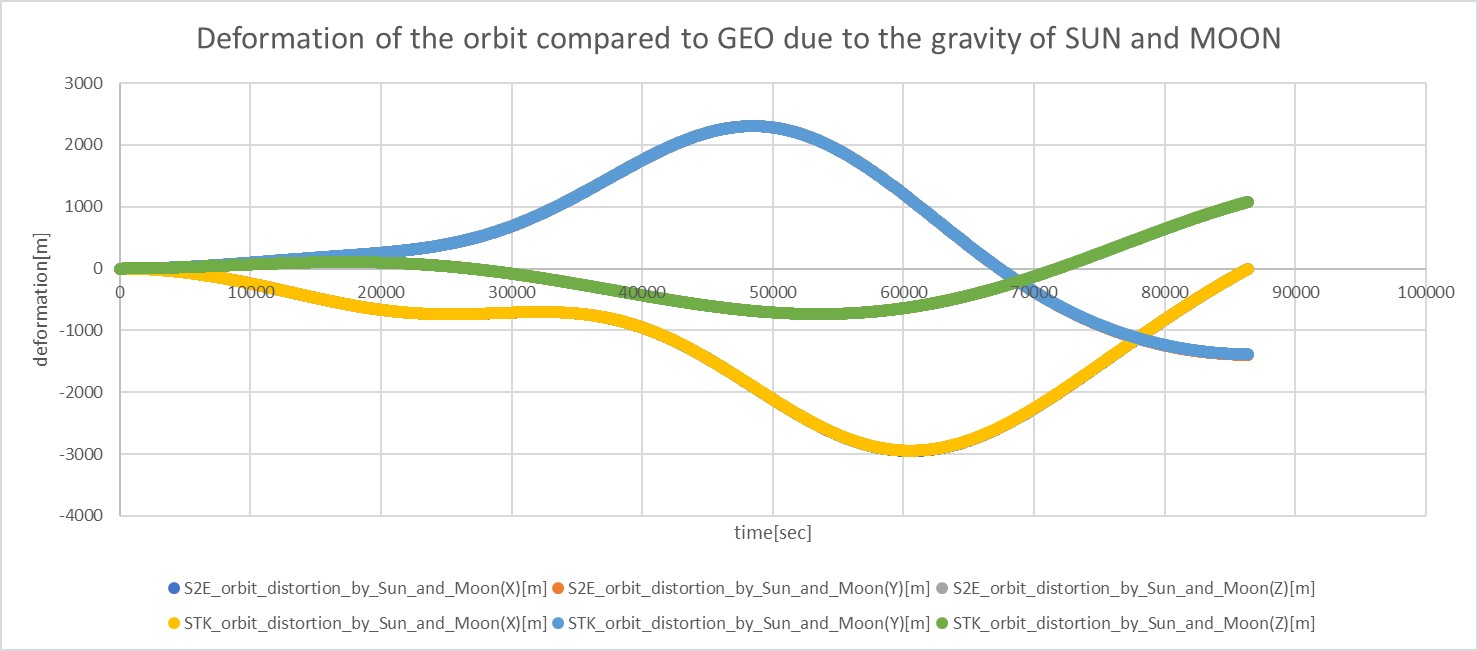
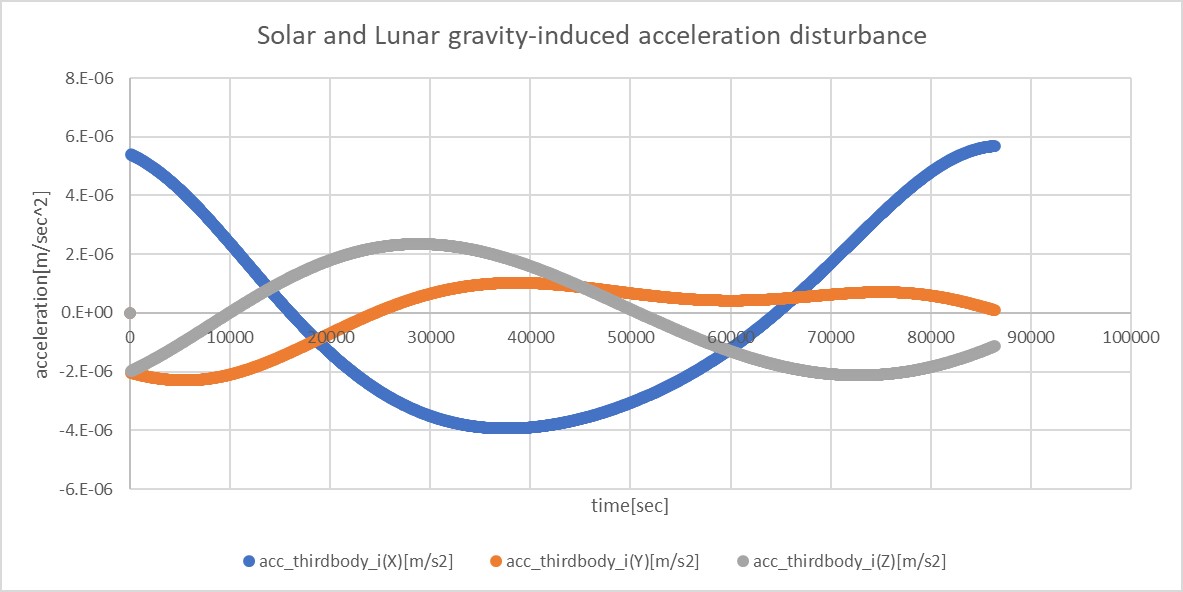
- The gravitational disturbance of both the Sun and the Moon is shown in the following figure.
- In all of the above cases, the S2E and STK results are consistent.
4. References
- Satellite Orbits chapter 3.3.