Specification for Relative Orbit propagation
1. Overview
1. functions
- The
RelativeOrbitclass calculates the position of a satellite with respect to a reference satellite. This class calculates the position both in the LVLH frame and inertial frame. Users can choose the update method between:- relative dynamics propagation using RK4
- update using STM(State Transition Matrix)
2. Related files
src/dynamics/orbit/orbit.hpp, cpp- Definition of
Orbitbase class
- Definition of
src/dynamics/orbit/initialize_orbit.hpp, .cpp- Make an instance of orbit class.
src/dynamics/orbit/relative_orbit.hpp, .cpp- Definition of the class
- Libraries
src/library/orbit/relative_orbit_models.hpp, .cpp
- Library to store equations for various relative dynamics
3. How to use
-
Relative orbit propagation is available only when multiple satellites are simulated.
- The sample case in S2E_CORE simulates a single satellite. For an example of simulating multiple satellites, please refer to the tutorial.
-
Confirm the instance of
RelativeInformationis the member of each satellite. -
Set up the configuration of the
[ORBIT]section in thesample_spacecraft.ini.- Set
propagate_mode = RELATIVEto use the relative orbit propagation - Choose
relative_orbit_update_method.relative_orbit_update_method = 0means the orbit is updated with the propagation of the relative dynamics equation( $\dot{\boldsymbol{x}}=\boldsymbol{Ax}+\boldsymbol{Bu}$ , i.e., Hill equation).relative_orbit_update_method = 1means the orbit is updated with the STM( $\boldsymbol{x}(t)=\boldsymbol{\Phi}(t,t_0)\boldsymbol{x}(t_0)$ , i.e., Clohessy-Wiltshire solution).
- When you choose
relative_orbit_update_method = 0, setrelative_dynamics_model_type. - When you choose
relative_orbit_update_method = 1, setstm_model_type. - Set the initial relative position of the satellite in the LVLH frame. LVLH frame definition is:
- $\boldsymbol{x}$ is a direction vector from the reference satellite ("chief" in the figure) radially outward.
- The direction of $\boldsymbol{z}$ corresponds to the angular momentum vector of the reference satellite orbit.
- The direction of $\boldsymbol{y}$ is determined by $\boldsymbol{z}\times\boldsymbol{x}$.
Definition of LVLH frame [1] - Set the ID and ini file name of the reference satellite.
- NOTE: Confirm the
propagate_modeof the reference satellite is not 2. The orbit of the reference satellite must be propagated by the methods other than the relative orbit propagation.
- NOTE: Confirm the
- Set
4. How to add a new relative dynamics model
- New Relative Dynamics equation
- Add the name of the dynamics model to the
RelativeOrbitModelenum inrelative_orbit_models.hpp. - Add the function to calculate the system matrix like
CalcHillSystemMatrixinrelative_orbit_models.hpp. - Edit the
CalculateSystemMatrixfunction inrelative_orbit.hpp.
- New STM
- Add the name of the dynamics model to
StmModelenum inrelative_orbit_models.hpp. - Add the function to calculate the system matrix as
CalcHcwStminrelative_orbit_models.hpp. - Edit the
CalculateStmfunction inrelative_orbit.hpp.
2. Explanation of Algorithm
1. InitializeState
1. overview
- The
InitializeStatefunction initializes the orbit of the satellite.
2. inputs and outputs
- input
relative_position_lvlh_m,relative_velocity_lvlh_m_s
- The initial state of the satellite
gravity_constant_m3_s2- The gravity constant of the reference celestial body $\mu$
initial_time_s- Initial simulation time (default value is 0)
- output
- none
3. algorithm
4. note
2. CalculateSystemMatrix
1. overview
- The
CalculateSystemMatrixfunction is used only inside theRelativeOrbitclass. This function calls the system matrix calculation function according torelative_dynamics_model_type.
2. inputs and outputs
- input
relative_dynamics_model_type- The type of relative dynamics model
reference_sat_orbit- The orbit of the reference satellite
gravity_constant_m3_s2- The gravity constant $\mu$
- output
- none
3. algorithm
4. note
3. CalculateStm
1. overview
- The
CalculateStmfunction is used only inside theRelativeOrbitclass. This function calls the system matrix calculation function according tostm_model_type.
2. inputs and outputs
- input
stm_model_type- The type of relative dynamics model
reference_sat_orbit- The orbit of the reference satellite
gravity_constant_m3_s2- The gravity constant $\mu$
elapsed_sec- Elapsed simulation time
- output
- none
3. algorithm
4. note
4. CalculateHillSystemMatrix
1. overview
- The
CalculateHillSystemMatrixfunction calculates the system matrix of the Hill equation. - This function is declared in
relative_orbit_models.hppand is used by the
2. inputs and outputs
- input
orbit_radius- Radius of the reference satellite orbit $R$
gravity_constant_m3_s2- The gravity constant $\mu$
- output
system_matrix- system matrix
3. algorithm
- The mean motion of the reference orbit ($n$) is calculated as follows:
\[ n=\sqrt{\frac{\mu}{R^3}} \]
- Then, the system matrix ($\boldsymbol{A}$) is calculated as follows:
\[ \boldsymbol{A}= \begin{pmatrix} 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ 3n^2 & 0 & 0 & 0 & 2n & 0 \\ 0 & 0 & 0 & -2n & 0 & 0 \\ 0 & 0 & -n^2 & 0 & 0 & 0 \\ \end{pmatrix} \]
4. note
5. CalculateHcwStm
1. overview
- The
CalculateHcwStmfunction calculates the Hill-Clohessy-Wiltshire STM. - This function is declared in
relative_orbit_models.hppand is used by the
2. inputs and outputs
- input
orbit_radius- Radius of the reference satellite orbit $R$
gravity_constant_m3_s2- The gravity constant $\mu$
elapsed_sec- Elapsed simulation time
- output
system_matrix- system matrix
3. algorithm
- The mean motion of the reference orbit ($n$) is calculated as follows:
\[ n=\sqrt{\frac{\mu}{R^3}} \]
- Then, the system matrix ($\boldsymbol{A}$) is calculated as follows:
\[ \boldsymbol{\Phi}(t,t0)= \begin{pmatrix} 4-3\cos(nt) & 0 & 0 & \frac{\sin(nt)}{n} & \frac{2}{n}-\frac{2\cos(nt)}{n} & 0 \\ -6nt+6\sin(nt) & 1 & 0 & -\frac{2}{n}+\frac{2\cos(nt)}{n} & \frac{4\sin(nt)}{n}-3t & 0 \\ 0 & 0 & \cos(nt) & 0 & 0 & \frac{\sin(nt)}{n} \\ 3n\sin(nt) & 0 & 0 & cos(nt) & 2\sin(nt) & 0 \\ -6n+6n\cos(nt) & 0 & 0 & -2\sin(nt) & -3+4\cos(nt) & 0 \\ 0 & 0 & -n\sin(nt) & 0 & 0 & \cos(nt) \\ \end{pmatrix} \]
4. note
3. Results of verifications
1. Relative Orbit Propagation
1. overview
- Make sure the relative orbit is correctly propagated using a simple orbit
2. conditions for the verification
- input files
- Initialization files for the two satellites were prepared.
satellite0.inisatellite1.ini
- Initialization files for the two satellites were prepared.
- initial values
-
The orbit of the reference satellite (satellite0) is GEO. The initial position of the satellite (satellite1) is $(0\mathrm{m}, 100\mathrm{m}, 0\mathrm{m})^\mathrm{T}$ in LVLH frame. The orbit was propagated for 86400 sec (the period of GEO).
-
satellite0.inipropagate_mode = RK4 //Information used for orbital propagation by the Runge-Kutta method/////////// //initial satellite position[m] //*The coordinate system is defined in PlanetSelect.ini initial_position_i_m(0) = 4.2164140100E+07 //radius of GEO initial_position_i_m(1) = 0 initial_position_i_m(2) = 0 //initial satellite velocity[m/s] //*The coordinate system is defined in PlanetSelect.ini initial_velocity_i_m_s(0) = 0 initial_velocity_i_m_s(1) = 3.074661E+03 //Speed of a spacecraft in GEO initial_velocity_i_m_s(2) = 0 /////////////////////////////////////////////////////////////////////////////// -
satellite1.inipropagate_mode = RELATIVE //Information used for relative orbit propagation////////////////////////////// //Relative Orbit Update Method (0 means RK4, 1 means STM) relative_orbit_update_method = 0 // RK4 Relative Dynamics model type (only valid for RK4 update) // 0: Hill relative_dynamics_model_type = 0 // STM Relative Dynamics model type (only valid for STM update) // 0: HCW stm_model_type = 0 // Initial satellite position relative to the reference satellite in LVLH frame[m] // * The coordinate system is defined at [PLANET_SELECTION] in SampleSimBase.ini initial_relative_position_lvlh_m(0) = 0.0 initial_relative_position_lvlh_m(1) = 100.0 initial_relative_position_lvlh_m(2) = 0.0 // initial satellite velocity relative to the reference satellite in LVLH frame[m/s] initial_relative_velocity_lvlh_m_s(0) = 0.0 initial_relative_velocity_lvlh_m_s(1) = 0.0 initial_relative_velocity_lvlh_m_s(2) = 0.0 // information of reference satellite reference_satellite_id = 0 ///////////////////////////////////////////////////////////////////////////////
-
3. results
- The position of satellite1 seen from satellite0 in the inertia frame was calculated.
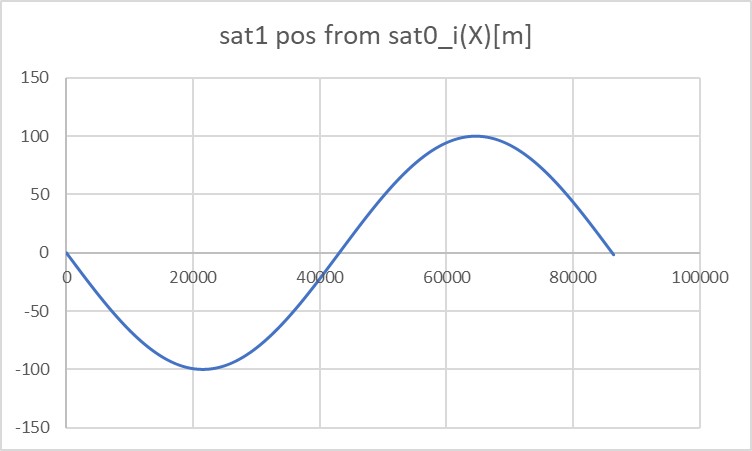
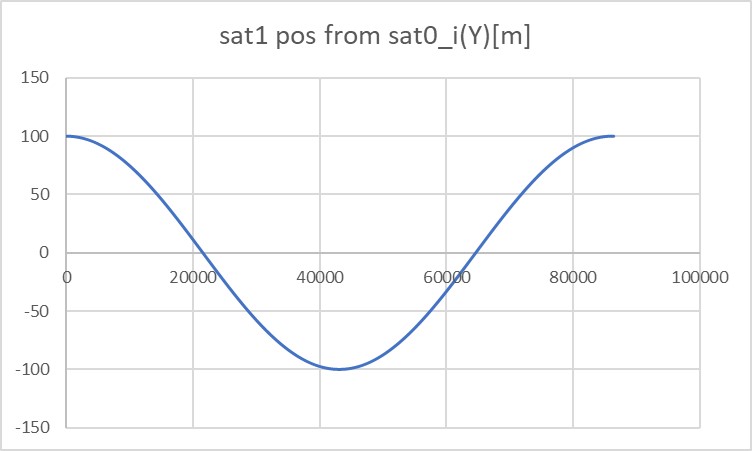
- They correctly move periodically.
- In this example of verification, the RK4 method is used to propagate relative orbits, but the results were the same when using STM.
4. References
- Kapila, V., Sparks, A. G., Buffington, J. M., & Yan, Q. (2000). Spacecraft formation flying: Dynamics and control. Journal of Guidance, Control, and Dynamics, 23(3), 561-564.