Specification for Solar Radiation Pressure Environment

1. Overview

1. Functions

SolarRadiationPressureEnvironment calculates solar power flux at the spacecraft's position, including the earth's eclipse effect.

src/environment/local/solar_radiation_pressure_environment.cpp, .hpp
- SolarRadiationPressureEnvironment class is defined.
src/environment/local/local_environment.cpp, .hpp
- SolarRadiationPressureEnvironment class is used here as a member variable of LocalEnvironment class.

3. How to use

Call UpdateAllStates function to calculates solar power flux and updates the eclipse flag.
Users can get calculated values by using the following functions:
- GetPressure_N_m2: Return solar pressure (N/m2) with eclipse effect for SRP disturbance calculation.
- GetPowerDensity_W_m2: Return solar power density (W/m2) with eclipse effect for Electrical Power System calculation.
- GetPressureWithoutEclipse_Nm2: Return solar pressure (N/m2) without eclipse effect.
- GetSolarConstant_W_m2: Return solar constant value 1366 [W/m2]
- GetShadowCoefficient: Return shadow function $\nu$.
  - When the spacecraft is in umbra, $\nu=0$.
  - When the spacecraft is in sunlight, $\nu=1$.
  - When the spacecraft is in penumbra, $0<\nu<1$.
- GetIsEclipsed: Return eclipse or not

2. Explanation of Algorithm

1. Pressure calculation in `UpdateAllStates` function

1. overview

Solar radiation pressure at the position of the spacecraft is calculated by using the inverse square law.

2. inputs and outputs

Constants
- Solar constant: $P_{\odot} = 1366$ W/m2
- Speed of light: $c = 299792458$ m/s
- Astronomical Unit: $AU = 149597870700$ m
Input variables
- The sun position in the body-fixed frame of the spacecraft: $\boldsymbol{r}_{\odot-sc}$ m
  - Unbold $r_{\odot-sc}$ is the norm of $\boldsymbol{r}_{\odot-sc}$
Output
Solar radiation pressure: $P_{sc}$ N/m2

3. algorithm

\[ P_{sc}=\frac{P_{sun}}{c}\left(\frac{AU}{r_{\odot-sc}}\right)^{2} \]

4. note

It is known that the solar constant value varies between 1365 and 1367 W/m2, but it is handled as a constant value in S2E.

2. `CalcShadowCoefficient` function

1. overview

This function determines that the spacecraft is inside the eclipse of the earth or not.

2. inputs and outputs

Constants
- Radius of the earth: $r_{\oplus}=6378137$ m
- Radius of the sun: $r_{\odot}=6.96\times10^{8}$ m
Input variables
- The sun position in the body-fixed frame of the spacecraft: $\boldsymbol{r}_{\odot-sc}$ m
- The earth position in the body-fixed frame of the spacecraft: $\boldsymbol{r}_{\oplus-sc}$ m
Output
- none

\[ \begin{align} A_{\odot} &= \sin^{-1}\left(\frac{r_{\odot}}{r_{\odot-sc}}\right)\\ A_{\oplus} &= \sin^{-1}\left(\frac{r_{\oplus}}{r_{\oplus-sc}}\right)\\ \delta &= \cos^{-1}\left(\frac{r_{\odot-sc}}{r_{\oplus-sc}}\cdot \boldsymbol{r}_{\oplus-sc}\cdot(\boldsymbol{r}_{\odot-sc}-\boldsymbol{r}_{\oplus-sc})\right)\\ \end{align} \]

4. note

See the following description of the CalcShadowFunction for the calculation of the shadow function.

3. `CalcShadowFunction` function

1. overview

This function calculates the degree of the Sun's occultation by the Earth.
The base algorithm is referred to Satellite Orbits chapter 3.4.

2. inputs and outputs

Input
- The apparent radius of the Sun: $A_{\odot}$
- The apparent radius of the Earth: $A_{\oplus}$
- The apparent separation of the centers of the Sun and the Earth: $\delta$
- The angle between the center of the Sun and the common chord: $x$
- The length of the common chord of the apparent solar disk and apparent celestial disk: $y$
Output
- The shadow function: $\nu$

3. algorithm

If the occultation is total, then $\nu=0$.
If the occultation is partial but maximum, then $\nu=1-\left(\frac{A_{\oplus}}{A_{\odot}}\right)^2$
If the occultation is partial, then $\nu = 1-\frac{S}{\pi A^2_{\odot}}$
- S is given by the following calculation.

\[ S=A_{\odot}^2\arccos\left(\frac{x}{A_{\odot}}\right)+A_{\oplus}^2\arccos\left(\frac{\delta-x}{A_{\oplus}}\right)-\delta\cdot y \]

In other cases, since it means that no occultation takes place, then $\nu=1$.

3. Results of verifications

1. Verification of pressure calculation in `UpdateAllStates` function

1. overview

The pressure calculation above is verified.

2. conditions for the verification

A test code written in the SRPEnvironment.cpp is used.
The sun position and the earth position are fixed, and the spacecraft position varies as following values.
- Sun-spacecraft distance: 149604270700m - 153797870700m
- Earth-spacecraft distance: 6400000m - 4200000000m

3. results

The pressure calculation is verified.

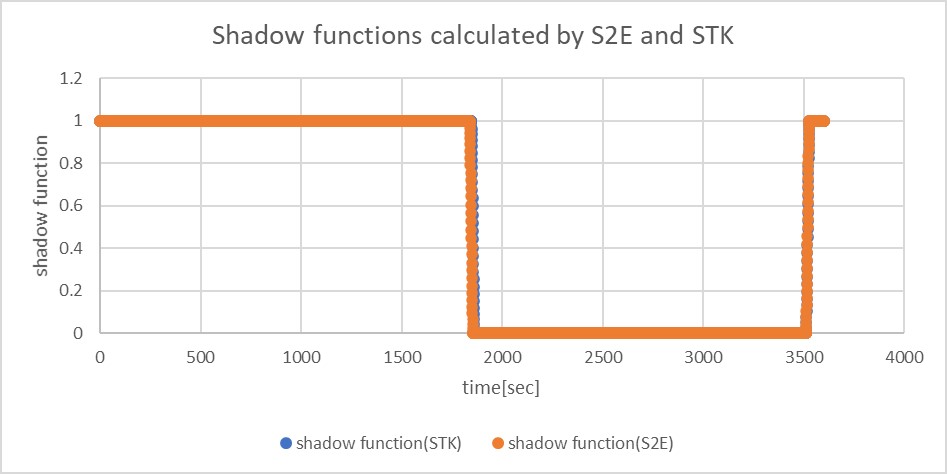
2. Verification of calculation in `CalcShadowFunction` function

1. overview

The calculation of the shadow function is verified.
The result of the CalcShadowFunction of S2E is compared with the results of the solar intensity of STK.

2. conditions for the verification

Orbit

The orbit of the ISS was used for verification.
The TLE data are as follows.

1 25544U 98067A   20250.86981481  .00000008  00000-0  82464-5 0  9991
2 25544  51.6470 304.2415 0002004  86.5035 251.6018 15.49214189244677

Simulation time

The simulation time is as follows.

//Simulation start date，[UTC]
StartYMDHMS=2020/09/13 12:00:00.0
//Simulation finish time，[sec]
EndTimeSec=3600

3. Results

The calculation of the shadow function is verified.

4. References

Montenbruck, O., Gill, E., & Lutze, F. (2002). Satellite orbits: models, methods, and applications. Appl. Mech. Rev., 55(2), B27-B28.

S2E documents