Surface Force: Solar Radiation Pressure disturbance
1. Overview
1. Functions
SolarRadiationPressureDisturbanceclass inheritsSurfaceForcebase class and calculates air drag disturbance force and torque.
2. Related files
solar_radiation_pressure_disturbance.cpp,solar_radiation_pressure_disturbance.hpp: TheSolarRadiationPressureDisturbanceclass is defined.surface_force.cpp,surface_force.hpp: The base classSurfaceForceis defined.- Note:
SurfaceForceclass inheritsSimpleDisturbanceclass, andSimpleDisturbanceclass inheritsDisturbanceclass. So, please refer them if users want to understand the structure deeply.
- Note:
disturbance.ini: Initialization file
3. How to use
- Make an instance of the
SolarRadiationPressureDisturbanceclass inInitializeInstancesfunction indisturbances.cpp- Create an instance by using the initialization function
InitSolarRadiationPressureDisturbance
- Create an instance by using the initialization function
- Set the parameters in the
disturbance.ini- Select
ENABLEforcalculationandlogging
- Select
2. Explanation of Algorithm
1. CalcCoefficients function
1. overview
CalcCoefficientscalculates the normal and in-plane coefficients forSurfaceForcecalculation.
2. inputs and outputs
- inputs
- $v_{s}$:Direction vector of the sun (spacecraft to the sun) at the body frame
- $P$ Solar pressure at the position of the spacecraft [N/m^2]
- setting parameters
- $\nu$ : Total reflectance
- $\nu = 1-\alpha$, where $\alpha$ is the absorption of the sun spectrum.
- $\mu$ : Specularity. Ratio of specular reflection inside the total reflected light.
- $A$ : Area of the surface
- $\nu$ : Total reflectance
- outputs
- $C_{n}$ and $C_{t}$
3. algorithm
- $C_{n}$ and $C_{t}$ are calculated as follows:
- $\theta$ is the angle between the normal vector and the sun vector.
\[ \begin{align} C_{n} &= AP \left((1+\nu\mu)\cos^{2}{\theta}+\frac{2}{3}\nu(1-\mu)\cos{\theta} \right)\\ C_{t} &= AP(1-\nu\mu)\cos{\theta}\sin{\theta} \end{align} \]
4. note
- NA
3. Results of verifications
1. Verification of perfect reflection case
1. overview
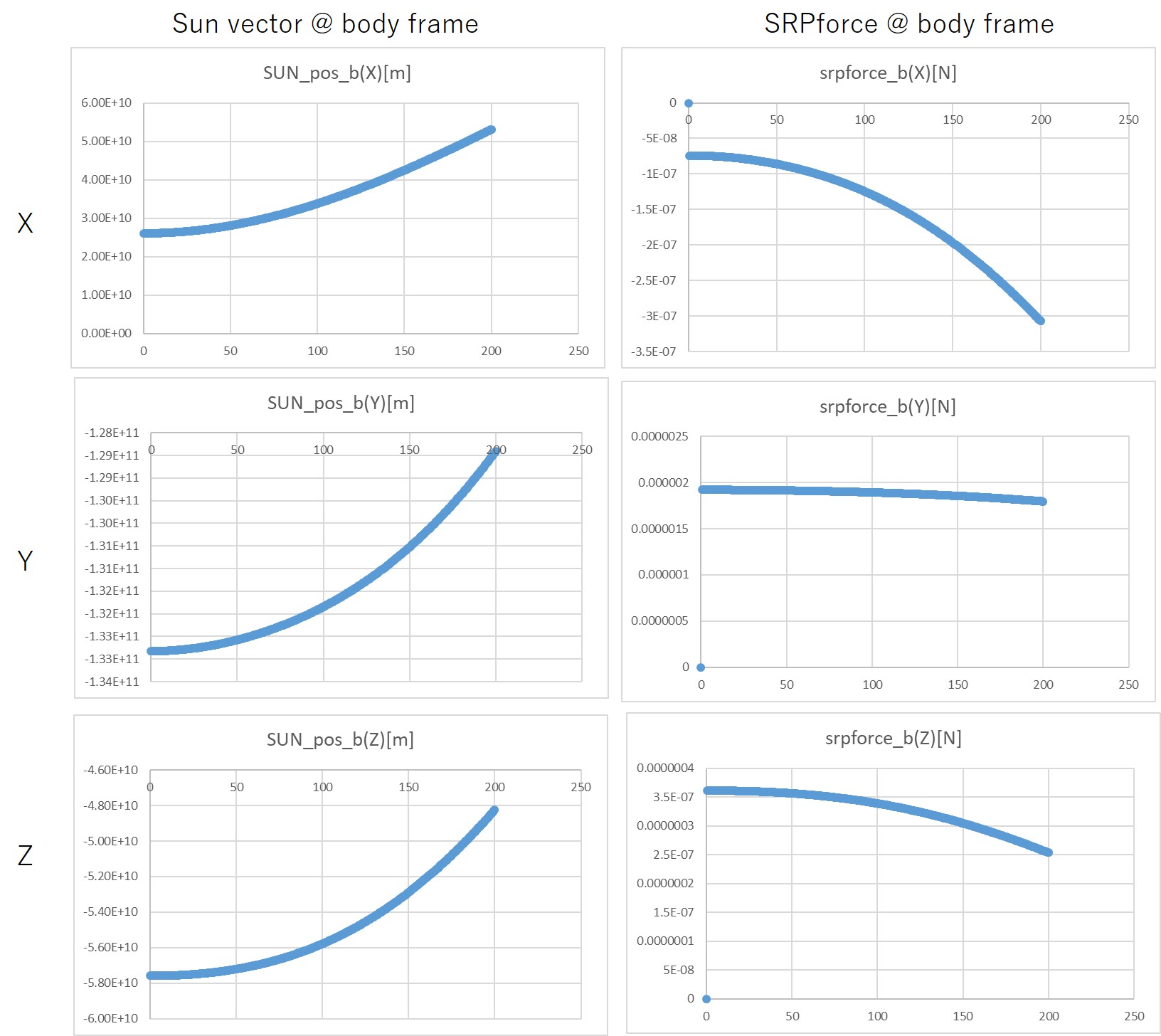
- In the perfect reflection case, the direction of the SRP force will be opposite from the direction of the sun.
2. conditions for the verification
- We assumed that the structure of the spacecraft is a 50-cm cube whose optical property is the perfect specular reflection($\nu=\mu=1$).
3. results
- We confirmed that the direction of the SRP force is opposite from the direction of the sun at the body frame.
4. References
- NA